soal geometri

Bagi pecinta matematika yang masih bingung menghadapi soal geometri berikut adalah contoh soalnya dan jika masih bingung boleh ditanyakan di hafiruddin anak ma_dah sampurnan bungh gresik :

1.	Pada gambar berikut, D terletak pada AB dan E pada AC sedemikian hingga DE sejajar BC. Jika DE = 1, BC = 6, AE = x, and EC = x2 + 4. Tentukan semua nilai yang mungkin untuk x!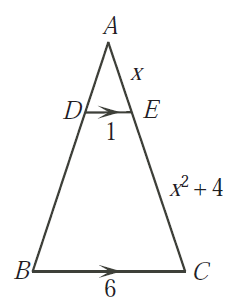

2.	Persegi panjang ABCD memotong sebuah lingkaran pada titik E, F,G, dan H, seperti pada gambar berikut. Jika AH = 4, HG = 5 dan BE = 3, tentukan panjang EF.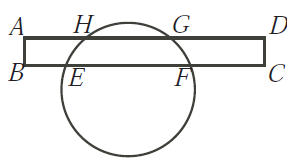

3.	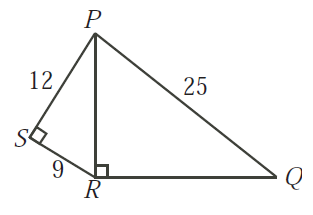Pada gambar di atas, segitiga PSR adalah segitiga siku-siku dan S sebagai sudut siku-siku. Dan segitiga PRQ juga merupakan segitiga siku-siku dengan R sebagai sudut siku-siku. Jika PS = 12, SR = 9, dan PQ = 25, tentukan panjang SQ!

4.	Pada gambar berikut, ABCD adalah persegi panjang dengan titik A terletak pada garis y = x + 10, titik B pada garis y = −2x + 10, dan C serta D pada sumbu- x. Jika AD = 4, berapakah luas persegi panjang ABCD?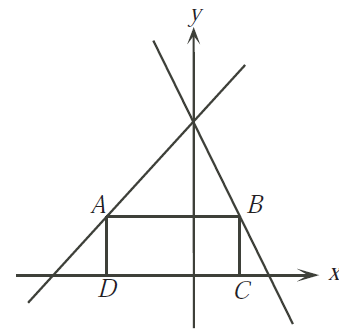

5.	Pada gambar berikut, O adalah pusat lingkaran. AN menyinggung lingkaran pada titik A, P terletak pada lingkaran, dan PN tegaklurus AN. Jika  AN = 15 dan PN = 9, tentukan jari-jari lingkaran!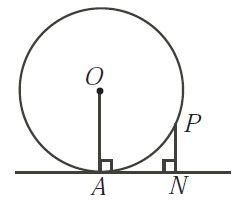

6.	Pada gambar berikut, ∠ABC = ∠BCD = 900. Jika, AB = 9, BC = 24 dan CD = 18. Serta diagonal AC dan BD dari segiempat ABCD berpotongan di titik E, tentukan luas ΔDAE!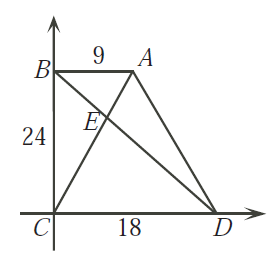

7.	Pada ΔABC, M adalah titik tengah BC, seperti pada gambar. Jika ∠ABM = 150dan ∠AMC = 300, tentukan ukuran ∠BCA?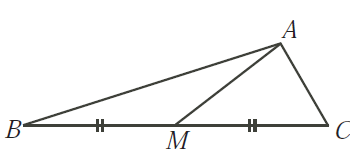

8.	Pada gambar berikut, lingkaran dengan persamaan x2 + y2 = 25 memotong sumbu-x pada titik A dan B. Garis x = 11 memotong sumbu-x pada titik C. Titik P bergerak pada garis x = 11 di atas sumbu-x dan AP memotong lingkaran pada titik Q. Tentukan koordinat titik P sedemikian hingga luas ΔAQB adalah ¼ luas ΔAPC.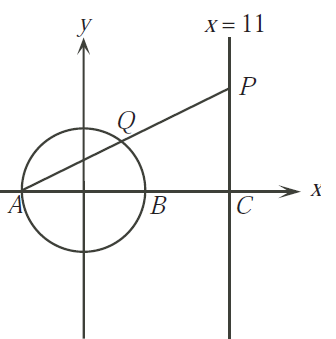

9.	Pada gambar berikut, Trapesium ABCD memiliki dua sisi sejajar yaitu AB dan DC dengan panjang 10 dan 20. Jika AD = 6 dan BC = 8, tentukan luas trapesium ABCD?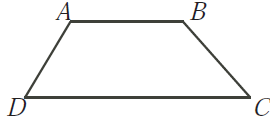

10.	Pada gambar berikut, PQRS adalah persegi panjang, dan T adalah titik tengah RS. Lingkaran dalam dari ΔPTS dan ΔRTQ masing-masing berjari-jari 3. Sedangkan lingkaran dalam dari ΔQPT berjari-jari 4. Tentukan ukuran persegi panjang PQRS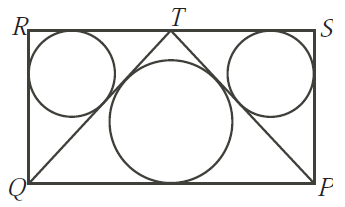

salamat mencoba !!!